Does ML make prediction simpler (i.e., allowing us to treat systems as blackboxes) and general (i.e., across a range of applications and use-cases)? The answer is NO.
Core idea
实验探究机器学习对黑盒系统性能预测 (treat the application as a black-box and remain agnostic to the prediction’s use-case) 的作用.
Methodology
- Metrics
-
Parameters: Application-level input, Application-level configuration, Infrastructure
-
Tests
The Best-Case (BC) Test: making very strong assumptions on both the systems and ML front, including one-feature-at-a-time assumption, seen configuration assumption, no-contention requirement and identical-inputs assumption.
The Beyond Best-Case (BBC) Test: relax each of the constraints/assumptions imposed in the BC test to study prediction accuracy under more realistic scenarios.
Application profiling and model training. In the profiling stage, an application is run under different configurations to generate raw dataseet. In the training stage, the dataset first undergoes pre-processing (featurization, normalization, and outlier removal), and is then randomly split into two disjoint datasets: the training set and the test set. Six ML algorithms are selected: k-nearest neighbors, random forest regression, linear regression, linear support vector machine (SVM) regression, kernelized SVM regression, and neural networks.
-
Predictors
The Best-of-Models (BoM) predictor: best-of-models error (BoM-err) as the minimum rMSRE across all the models we consider.
The Oracle predictor: O-err
\(f_{oracle}(X) = (\sum_{i=1}^n\frac{\delta(X_{i},X)}{Y_{i}}) / (\sum_{i=1}^n\frac{\delta(X_{i},X)}{Y_{i}^2})\) \(\delta(a,b) = 1 \quad \quad if \quad a= b,\quad and \quad 0 \quad otherwise\)
O-err captures the irreducible error inherent to an application (i.e., no ML model could achieve an error rate lower than the O-err) while the BoM-err captures the lowest error rate achieved by some ML model.
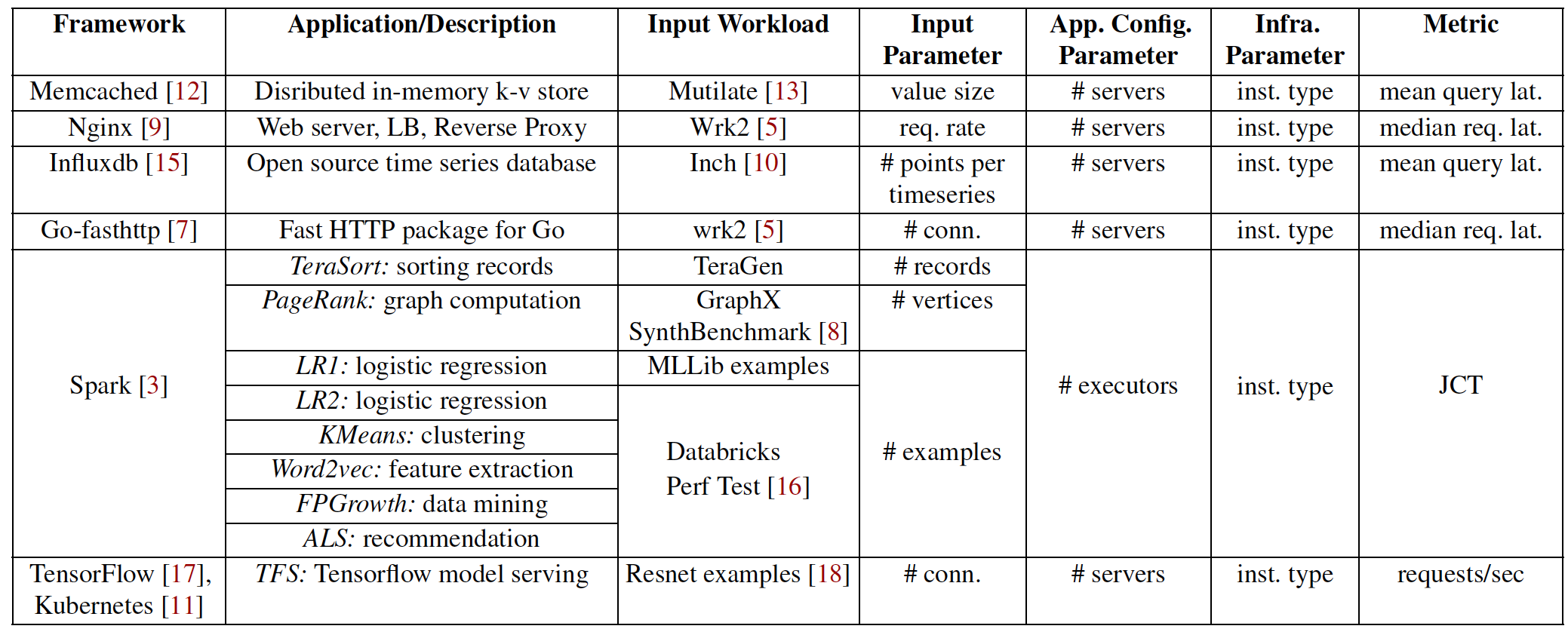
Results: Existing Applications
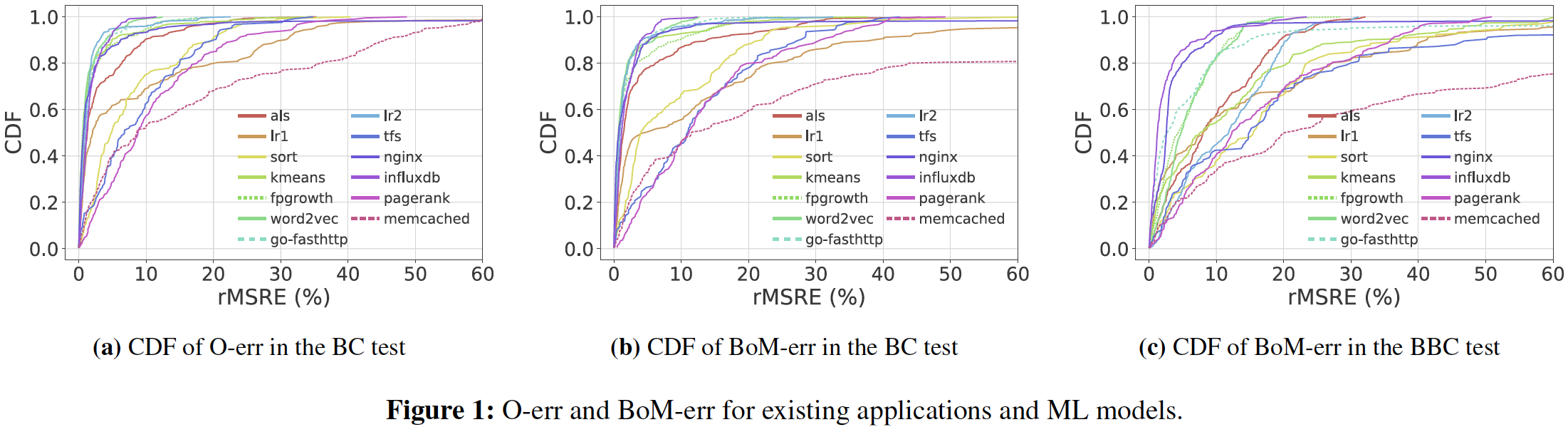
Results: Modified Applications
If these sources of irreducible errors are identified and eliminated, to what extent would it improve performance predictability ?
Probabilistic Predictions
Implications and Takeways
-
Irreducible errors may be attributed to two common design techniques: 1) the use of randomization (e.g., in load-balancing, scheduling) ; 2) the use of system optimizations in which a new mode of behavior is triggered by a threshold parameter (e.g., a promotion estimate, timeouts, a threshold on available workers).
-
Application modifications to eliminate sources of irreducible errors do produce a notable increase in prediction accuracy. However, in more realistic BBC scenarios, prediction errors do remain high for certain applications due to the underlying trend being difficult to learn.
-
While ML fails to meet the goal of generality, we did find several scenarios where ML-based prediction was effective, showing that we must apply ML in a more nuanced manner by first identifying whether/when ML-based prediction is effective.
-
Comparing ML Models: 1) No clear winner: no ML model performs the best across all prediction scenarios and across all applications; 2) No clear loser either: each model performs the best for at least one prediction scenario or application; 3) Neural network often results in the best performance or has error rates close to the best performing model; 4) For cases where neural network performed the best, there was often at least one other simpler model performed as well.